Lastnosti dokumenta
- Naslov
- MPI
- Del
- Iskanje praštevil
- Datum vsebine
- 01. 06. 2007
- Original
- mpi.pdf
- Vrsta
- seminarska naloga
- Jezik
- slovenščina
- Različica
- 1.0
- Ustanova
- Fakulteta za računalništvo in informatiko, Univerza v Ljubljani
- Študij
- Računalništvo in informatika, Logika in sistemi, 4. letnik
- Predmet
- Celularne strukture in sistemi
- Mentor
- dr. Branko Šter
- Avtor
- Tine Lesjak
- Ocena
- 10 od 5-10
Priloge
- sequential.c
- Sekvenčni algoritem
- parallelFullList.c
- Paralelni algoritem z uporabo MPI. Vsak proces alocira cel seznam števil.
- parallelOwnList.c
- Paralelni algoritem z uporabo MPI. Vsak proces alocira le svoj seznam števil.
Opis problema
Cilj naloge je napisati program z uporabo MPI (Message Passing Interface) orodja in knjižnic, ki na paralelni način poišče vsa praštevila od 2 do n (vključno).
Algoritem
Algoritem je razvit iz tako imenovanega Eratostenovega sita, ki je najpreprostejši (in najmanj učinkovit) algoritem za iskanje praštevil. Več informacij je na voljo na http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes.
Opis algoritma (sekvenčna oblika)
- Ustvari seznam neoznačenih naravnih števil od 2 do n.
- Postavi k=2 (prvo neoznačeno število v seznamu).
- Ponavljaj ... dokler k2 <= n.
- Označi vse večkratnike števila k od k2 do n.
- Poišči najmanjše neoznačeno število, ki je večje od k. Postavi k na to vrednost.
- Števila, ki so ostala neoznačena, so praštevila.
Primer iskanja praštevil do 42
k=2:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
k=3:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
k=5:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
Praštevila so torej 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 in 41.
Paralelna izvedba algoritma
- Vsak proces je odgovoren za del seznama števil.
- Proces i (procesi se štejejo od 0 dalje) vključuje elemente od
ceil(i(n+1)/p)doceil((i+1)(n+1)/p)-1(vključno), pri čemer je p število procesov. - Največje število (k), uporabljeno za sito, je
ceil(sqrt(n)).
| Št. procesa | Prvi element | Zadnji element | Dolžina seznama |
|---|---|---|---|
| 0 | 0 | 6 | 7 |
| 1 | 7 | 13 | 7 |
| 2 | 14 | 20 | 7 |
Tabela 1 - Primer porazdelitve seznama na 3 procese (p=3, n=20).
Program
Program sem najprej napisal v sekvenčni obliki, nato je sledila razširitev na paralelno. Na koncu sem razvil še izboljšano različico paralelnega algoritma, ki deluje tako, da vsak proces alocira le toliko pomnilnika, kot ga potrebuje za svoj seznam.
Za primer lahko povem, da je razlika precejšnja, saj v primeru iskanja do sto milijonov (n=100.000.000) vsak proces v boljši različici porabi le 10 MB pomnilnika, v prvi različici pa ima vsak proces celotno tabelo in tako porabi 100 MB pomnilnika.
Lastnosti programa
- n se vnese kot vhodni parameter programa.
- Vsak proces alocira le svoj seznam števil.
- Vsa sita so vedno v procesu 0. Le-ta jih razpošilja ostalim procesom s pomočjo MPI_Bcast (broadcast) funkcije. Če vsa sita niso v procesu 0, se program konča in javi napako.
- Program na koncu izpiše le število praštevil od 2 do n. Vsak proces vrne število praštevil v svojem delu, ki jih proces 0 na koncu sešteje s pomočjo funkcije MPI_Reduce.
- Program beleži trajanje izvajanja s pomočjo funkcije MPI_Barrier za usklajevanje procesov in MPI_Wtime za beleženje časa.
Program sem napisal v jeziku C. Razvijal sem ga v razvojnem okolju Dev-C++. Za MPI knjižnico sem vzel MPICH različice 1.2.5.
Izvorna koda
parallelOwnList.c
/*
* The parallel algorithm (the sieve of Eratosthenes) for searching prime
* numbers from 2 to n (inclusive) using MPI.
* In this version every process allocates its own list of numbers that is
* appropriate only for it.
* For example, if your search to 100 million with 10 processes, every process
* allocates only 10 MB of memory.
*
* @author TineL
* @version 1.0, 2007-06-01
*/
#include <stdio.h>
#include <stdlib.h>
#include "mpi.h"
typedef char boolean;
boolean true=1;
boolean false=0;
long n=100; // Default numbers to search to
int main(int argc, char *argv[]) {
double time; // Timing duration of execution
long i=0; // For loops
int me; // This process
int p; // Number of processes
// Read n from the program arguments
if (argc==2) {
n=strtoul(argv[1], NULL, 0);
}
// Init MPI
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &me);
MPI_Comm_size(MPI_COMM_WORLD, &p);
MPI_Barrier(MPI_COMM_WORLD); // Synchronize all processes
time=MPI_Wtime(); // Start timer
if (p>(int)sqrt(n)) {
if (me==0) printf("Error: Too many processes! Exiting...\n");
MPI_Finalize();
exit(1);
}
// Start
printf("Process %d started...\n", me);
// Everybody: Recognize my position
long from=me*(n+1)/p; // I have from this number further
long myN=(me+1)*(n+1)/p-1-from; // I have myN numbers to deal with
// Everybody: Allocate my list for numbers
boolean* marks=(boolean*)malloc(sizeof(boolean)*(myN+1));
if (marks==NULL) {
printf("Error: Cannot allocate enough memory. Exiting...\n");
exit(1);
}
// Everybody: Reset all my marks
for (i=0; i<=myN; i++) {
marks[i]=false;
}
if (me==0) {
marks[0]=true; // Number 0 is not a prime number
marks[1]=true; // Number 1 is not a prime number
}
// Start at number 2
long k=2;
while (true) {
MPI_Bcast(&k, 1, MPI_UNSIGNED_LONG, 0, MPI_COMM_WORLD);
// Everybody: Break loop if we are finished
if (k==0) break;
// Everybody: Mark all my multiples of k
for (i=k*k-from; i<=myN; i+=k) {
if (i>=0) marks[i]=true;
}
// Root: Find next smallest non-marked number
if (me==0) {
for (i=k+1; i<=myN; i++) {
if (marks[i]==false) {
k=i;
break;
}
}
if (i>myN||k*k>n) k=0; // Root: Not found or seed exceeds my
// interval - Finished
}
}
// Everybody: Count my prime numbers (non-marked numbers)
long myCount=0;
for (i=0; i<=myN; i++) {
if (marks[i]==false) myCount++;
}
printf("Process %d found %ld prime numbers.\n", me, myCount);
// Root: Sum all counts
long totalCount=0;
MPI_Reduce(&myCount, &totalCount, 1, MPI_UNSIGNED_LONG, MPI_SUM, 0,
MPI_COMM_WORLD);
time=MPI_Wtime()-time; // Stop timer
// Root: Print result
if (me==0) {
printf("Found %ld prime numbers from 2 to %ld in %f seconds.\n",
totalCount, n, time);
}
// End
printf("Process %d stopped.\n", me);
// Finish MPI
MPI_Finalize();
return 0;
}Meritve
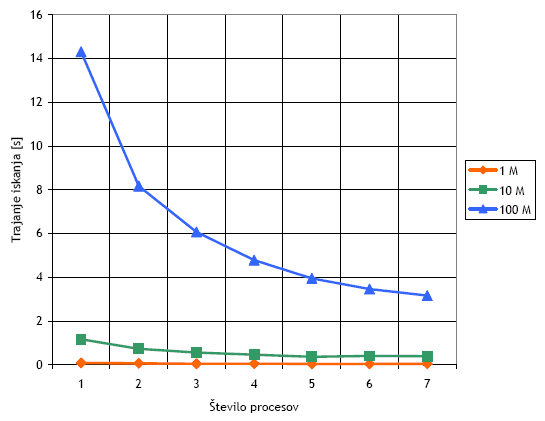
Meritve sva skupaj s sošolcem izvajala na gruči računalnikov v laboratoriju (LRI-1) fakultete. Računalniki so bili vrste Celeron 2,8 GHz z dovolj pomnilnika, med seboj povezani s 100 Mb/s Ethernet omrežjem. Meritve sva opravila na največ sedmih računalnikih, vsak proces je vedno tekel na svojem računalniku. Iskanje praštevil sva izvedla za tri primere: prvič sva iskala praštevila do milijon (1 M), drugič do deset milijonov (10 M) in tretjič do sto milijonov (100 M).
Graf 1 - Trajanje iskanja praštevil na več računalnikih.
Sklep
Če si ogledamo rezultate bolj podrobno, lahko opazimo, da pri izvajanju z do 5 procesi, trajanje paralelnega iskanja precej upada, kar je seveda pričakovano. Ko sva pa število procesov povečala na 6 ali 7, pohitritve praktično ni več - še več, pri n=1 M in n=10 M je iskanje trajalo celo dlje. Očitno je, da je davek, ki ga terja MPI komunikacija med procesi, prevelik in da se MPI splača uporabljati le na zelo velikih primerih oz. dolgotrajnih operacijah - v najinem primeru bi to lahko trdil le za n=100 M.
 §
§