Zahvala Kazalo Seznam uporabljenih kratic in simbolov 1 Povzetek 2 Abstract 3 Uvod 4 Opis problema 5 Načrt sistema 6 Podatkovni model 7 Geokodiranje 8 Nasprotno geokodiranje 9 Usmerjanje 10 Izkušnje in nadaljnje delo 11 Sklep Dodatek A Navodila za uporabo sistema Literatura
- Naslov
- Razvoj naprednih storitev za GIS
- Del
- 8 Nasprotno geokodiranje
- Datum vsebine
- 22. 11. 2009
- Original
- RazvojNaprednihStoritevZaGIS.pdf
- Vrsta
- diplomska naloga
- Jezik
- slovenščina
- Različica
- 1.0
- Ustanova
- Fakulteta za računalništvo in informatiko, Univerza v Ljubljani
- Študij
- Univerzitetni, računalništvo in informatika, logika in sistemi
- Predmet
- -
- Mentor
- doc. dr. Mojca Ciglarič
- Avtor
- Tine Lesjak
- Ocena
- 10 od 1-10
Gre za celotno diplomsko delo s predstavitvijo.
Dodatne objave dela:
- ePrints.FRI: ID 933
- COBISS: ID 7349844
- predstavitev.pdf
- Predstavitev diplomskega dela na zagovoru (dne 22. 10. 2009).
- projekti.zip
- Vsa izvorna koda v obliki SpringSource Tool Suite projektov (združljivi z Eclipseom) pod licenco Creative Commons Attribution 2.5 Slovenia License
- primeri.zip
- Primeri, predstavljeni kot izvlečki kode v diplomskem delu.
- tinel-gis-geocoding.war
- Storitev geokodiranja.
- tinel-gis-reversegeocoding.war
- Storitev nasprotnega geokodiranja.
- tinel-gis-routing.war
- Storitev usmerjanja.
Nasprotno geokodiranje (angl. reverse geocoding) je storitev, ki poišče geografske kraje, ki se nahajajo v neposredni bližini določene lokacije. Prav pride uporabnikom, ki na nek način pridobijo koordinate neke lokacije (npr. s klikom na karti, iz sprejemnika GPS ipd.) in bi radi izvedeli, kateri je najbližji geografski kraj (naslov, cesta, zgradba ipd.). Na primer, lastniku vozila se namesto geografskih koordinat v ustreznem grafičnem odjemalcu prikaže najbližji naslov, kjer stoji njegovo vozilo. Uporabniki si samo s koordinatami le stežka predstavljajo pravo lokacijo.
Nasprotno geokodiranje je, zanimivo, kljub podobnemu imenu tehnično precej drugače izvedeno od geokodiranja.
Ustrezna koda se nahaja v javinem paketu net.tinelstudio.gis.reversegeocoding.
8.1 Iskalci
Storitev nasprotnega geokodiranja je zasnovana tako, da odjemalec strežniku poda zahtevo v obliki iskalca (angl. locator). Iskalci imajo zelo podobno vlogo kot iskalci pri storitvi geokodiranja. Uporabnik v odjemalcu nastavi iskalca in ga kot parameter priloži metodi, ko kliče storitev nasprotnega geokodiranja.
Vsak iskalec ima tri parametre, ki jih je potrebno nastaviti:
- searchLocation - Geografski koordinati iskalne lokacije, podani v stopinjah, v obliki zemljepisne dolžine in širine. Npr. za Ljubljanski grad sta (14.508, 46.049).
- maxDistanceMeters - Iskalni radij, največja razdalja v metrih med iskalno lokacijo in krajem, ki še pride v poštev. S tem podatkom se omejimo samo na določeno območje okoli iskalne lokacije. Če je radij premajhen oz. v okolici iskalne lokacije ni kraja, iskalec vrne prazen seznam zadetkov. Iskalni radij je po navadi razmeroma majhen, govorimo o številki od nekaj sto metrov do nekaj kilometrov.
- maxResults - Največje število zadetkov. Če je 1, potem iskalec vrne le najbližji zadetek. Koristna omejitev, če je iskalni radij velik in je v okolici iskalne lokacije ogromno krajev (npr. v mestih).
Z izbiro iskalca uporabnik pove, katere kraje naj storitev išče.
Storitev pozna tri vrste iskalcev:
- Osnovni iskalec, ki išče samo po eni vrsti krajev.
- AddressLocator - Išče samo med naslovi (domena Address).
- StreetLocator - Išče samo med cestami (domena Street).
- BuildingLocator - Išče samo med zgradbami (domena Building).
- Multi iskalec, ki kombinira več iskalcev.
Iskalec najprej delegira iskanje prvemu podanemu iskalcu, nato drugemu, nato tretjemu in tako dalje. Zadetke vseh iskalcev vrne v enem seznamu po vrsti tako, kot so bili najdeni.- CompositeLocator - Delegira iskanje po vseh navedenih iskalcih.
- FullCompositeLocator - Predpripravljen iskalec, ki delegira iskanje po vseh osnovnih iskalcih.
- Multi iskalec, ki preide na naslednjega iskalca, če prejšnji ne vrne zadetkov.
Iskalec najprej delegira iskanje prvemu podanemu iskalcu. Če ta ne vrne nobenega zadetka, se iskanje delegira drugemu, drugače se takoj vrnejo zadetki samo prvega iskalca. Ostali sploh ne pridejo na vrsto.- FallbackLocator - Delegira iskanje po navedenih iskalcih, dokler eden ne vrne zadetkov.
- DefaultFallbackLocator - Predpripravljen iskalec, ki smiselno delegira iskanje po osnovnih iskalcih, dokler eden ne vrne zadetkov.
Z multi iskalci je možna zelo zapletena in fino nastavljiva kombinacija vseh iskalcev, tudi več multi iskalcev, npr.:
Locator locator=new FallbackLocator(new CompositeLocator(
new AddressLocator(), new BuildingLocator()), new StreetLocator());Koda 8.1: Primer bolj zapletene kombinacije iskalcev in multi iskalcev.
Vsakemu iskalcu lahko nastavimo največje število zadetkov (maxResults), ki jih vrne. V primeru sestavljenega iskalca (CompositeLocator) se iskanje prekine, ko je skupaj najdeno dovolj zadetkov. Drugače pa velja največje število zadetkov posameznega iskalca, če ga nastavimo. V kolikor največjega števila zadetkov za posameznega iskalca ne nastavimo, velja zanj število, ki smo ga nastavili za multi iskalca.
Locator locator=new AddressLocator();
locator.setSearchLocation(new Coordinate(15.654, 46.548));
locator.setMaxDistanceMeters(500);
locator.setMaxResults(10);
List<? extends Place> places=this.reverseGeocodingService
.findNearest(locator);Koda 8.2: Primer uporabe iskalca AddressLocator.
Na strežniški strani vsak iskalec naredi svoje delo. Vsak osnovni iskalec poišče zadetke neposredno v podatkovni zbirki. Multi iskalec samo uporabi osnovne iskalce, kar pomeni, da se poizvedba v zbirki požene večkrat, za vsakega osnovnega iskalca posebej.
8.2 Algoritem
Vsak osnovni iskalec vrne seznam najdenih krajev, ki ustrezajo kriterijem, sortiranih po oddaljenosti od iskalne lokacije tako, da ji je prvi kraj najbližje.
Kriteriji, ki so bistveni za algoritem, so trije:
- vrsta iskalca pove, v kateri(h) domeni(ah) se bo iskalo,
- parameter searchLocation pove iskalno lokacijo, okoli katere se bo iskalo in
- parameter maxDistanceMeters pove največjo oddaljenost od iskalne lokacije, okoli katere se bo iskalo in sortiralo zadetke.
Zadovoljiti vsem tem kriterijem skupaj z največjo hitrostjo in natančnostjo je žal nemogoče. Poglejmo, zakaj.
Geografski kraji so prostorski podatki sestavljeni iz točk (angl. point), ki so podane z geografskimi koordinatami v stopinjah. Prva koordinata je zemljepisna dolžina (angl. longitude). Druga je zemljepisna širina (angl. latitude). Pri iskanju najbližjih točk se najprej omejimo na neko največjo razdaljo med iskalno lokacijo in točkami (iskalni radij) in nato zadetke sortiramo glede na oddaljenost od iskalne lokacije.
Točke so izražene v (kotnih) stopinjah, iskalni radij v metrih. Ti enoti med seboj nista primerljivi.
Koordinate označujejo točno lokacijo na površini objekta, v našem primeru na površini Zemlje. Pri tem je ključna oblika tega objekta. Površina Zemlje je podobna sferi s fiksnim polmerom. Ampak sfera je le, sicer dokaj dober, približek, saj je Zemlja na polih rahlo sploščena, zato je v uporabi vrsta natančnejših elipsoidov. Eden najbolj uporabljanih je WGS 84, saj se uporablja pri tehnologiji GPS. Obliki objekta z referenčnimi točkami strokovno pravimo datum (angl. datum).
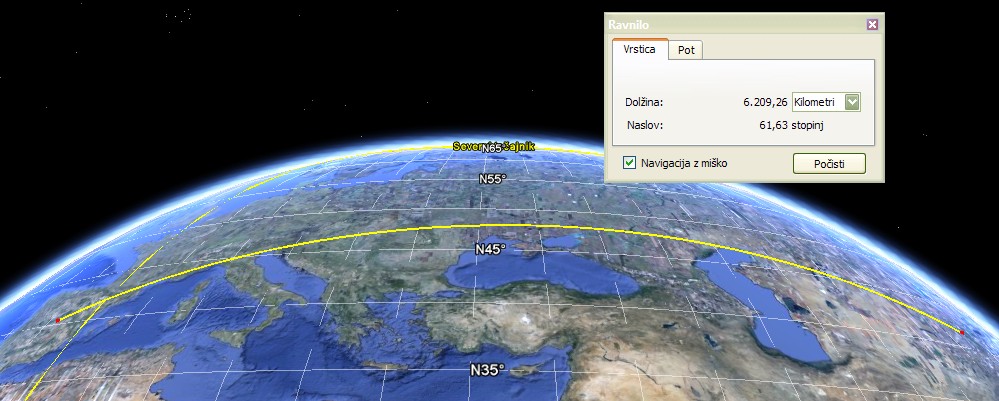
Najkrajšo razdaljo (angl. great-circle distance) med dvema lokacijama lahko izračunamo na dva načina. Pri prvem načinu razdalje računamo neposredno na modelu sfere ali elipsoida. Za računanje razdalj na sferi uporabimo nekaj kotnih funkcij, potrebujemo pa le podatek o polmeru sfere (Zemlje). Ker površina Zemlje ni sfera, je polmer le dogovorjen približek (npr. 6.371.007 m [19]). Če želimo nekoliko večjo natančnost, lahko razdalje računamo neposredno na elipsoidu. V poštev pridejo nekoliko težje matematične formule (v geodeziji se uporabljajo Vincentyjeve formule [11] [15]). Obe metodi sta natančni in uporabni za računanje razdalj kjerkoli na Zemlji.
Slika 8.1: Primer najkrajše razdalje med dvema lokacijama na Zemlji. Z rumeno upognjeno črto je označena najkrajša razdalja (6209 km), ki gre po površini Zemlje in ne skozi njo.
Pri drugem načinu lokacijo pretvorimo v metrični (kartezični) koordinatni sistem. Lokacijo s tridimenzionalnega objekta preslikamo v dvodimenzionalno ravnino. To imenujemo kartografska projekcija (angl. map projection). Obstaja ogromno projekcij. Ločijo se po različnih načinih projiciranja (valjni, azimutni, stožčni), različnih datumih (sfera ali elipsoid) in različnih enotah (metri, stopinje, milje ipd.). Težava vseh so različna popačenja, različna popačenja pa narekujejo različno uporabo.
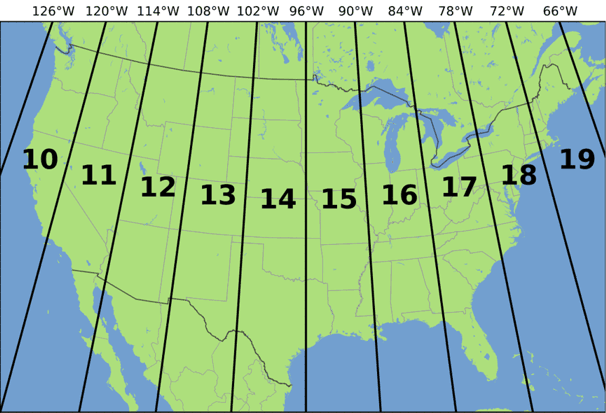
V našem primeru pridejo v poštev samo projekcije, pri katerih je razdalja v vse smeri pravilna. Ena takšnih je univerzalna prečna Merkatorjeva (angl. Universal Transverse Mercator - UTM) projekcija, ki je pravzaprav sistem več projekcij. Te so razdeljene v posamezne cone v mreži UTM, ki jo sestavlja 60 con za severno poloblo in 60 za južno. Vsaka zajema pas 6° zemljepisne dolžine. Projekcija v vsaki coni je zelo natančna, saj so popačenja na robovih le približno 1 % [1] [10]. Skupaj z univerzalnim polarnim stereografskim (angl. Universal Polar Stereographic - UPS) sistemom projekcij, ki zajema oba pola, imamo Zemljo v celoti pokrito in vsako lokacijo izraženo v metrih.
Težava nastane, kadar želimo izračunati razdaljo med dvema lokacijama, ki padeta v različne cone. Vsaka cona ima namreč drugo referenčno točko in lokacije med seboj niso primerljive. Lahko bi sicer uporabili eno cono za obe točki, a bi bile napake velike. Če bi uporabili projekcijo, ki pokriva večino Zemlje, npr. svetovno Merkatorjevo (angl. World Mercator), pa bi bile napake nesprejemljivo velike že na zemljepisni širini Slovenije, kaj šele bližje poloma. V kolikor bi se omejili na računanje razdalj samo po Sloveniji, bi bila projekcija UTM za cono 33 N odlična izbira, a kakor bi želeli pokukati izven Slovenije, po Evropi, bi naleteli na več kot 10 con.
Slika 8.2: Cone univerzalnega Merkatorjevega sistema (UTM) na območju ZDA. Razdalje med lokacijami znotraj ene cone so zelo natančne.
Pomembna lastnost sistema je hitrost iskanja krajev. Podatkovna zbirka PostgreSQL ima posebno vrsto indeksa primerno za prostorske podatke - GiST. Ker so kraji hranjeni v obliki točk v stopinjah, ki so indeksirane, to pomeni, da se pri iskanju uporabljajo indeksi samo takrat, ko iščemo v isti enoti, stopinjah. V našem primeru pa vedno iščemo v metrih. Torej, pri metodah za neposredno računanje na sferi ali elipsoidu se indeksi ne uporabljajo, oddaljenost iskalne lokacije se računa z vsakim krajem, kar pa je počasno.
Pri drugem načinu, projekciji, obstajata dve možnosti. Lahko sproti projiciramo kraje, a pri tem se indeksi ne uporabljajo, saj je treba vsak kraj najprej projicirati, šele nato se izračuna razdalja. Druga možnost je, da bi krajem dodali še en atribut v zbirki, in sicer iste točke, vendar v drugem, že projiciranem metričnem koordinatnem sistemu. Te točke bi indeksirali, iskanje bi potekalo neposredno po indeksih. A težava nastane pri izbiri tega metričnega sistema. Če bi izbrali edini dovolj natančen sistem UTM skupaj z UPS, potem vse točke ne bi bile v isti coni in ne bi bile primerljive med seboj.
Za lažjo primerjavo in preglednost sem nekaj možnih rešitev podal v tabelo 8.1:
| Metoda | Opis | Natančnost | Hitrost |
|---|---|---|---|
| A | sprotno projiciranje kraja v cono UTM/UPS od iskalne lokacije | velike napake v primeru, ko je kraj precej oddaljen od iskalne cone; velika natančnost, če je kraj v iskalni coni |
nizka hitrost: indeksi se ne uporabljajo, ker se kraji sproti projicirajo |
| B | sprotno projiciranje kraja v svetovno Merkatorjevo projekcijo | velike napake na zemljepisni širini proti poloma; pola nista podprta | nizka hitrost: indeksi se ne uporabljajo, ker se kraji sproti projicirajo |
| C | predprojicirane dodatne točke v svetovni Merkatorjevi projekciji | velike napake na zemljepisni širini proti poloma; pola nista podprta | visoka hitrost: neposredna uporaba indeksov |
| Č | računanje neposredno v stopinjah | razdalje v stopinjah niso primerljive z metri: natančnost ob ekvatorju, velike napake proti poloma | visoka hitrost: neposredna uporaba indeksov |
| D | računanje neposredno na sferi ali elipsoidu | velika natančnost | nizka hitrost: indeksi se ne uporabljajo, ker se razdalje sproti računajo |
Tabela 8.1: Metode za računanje najkrajše razdalje med iskalno lokacijo in geografskimi kraji.
Algoritem temelji na metodi D, saj je edina brezpogojno natančna za cel svet. PostGIS ima za ta namen pripravljeni dve funkciji [24]: ST_distance_sphere in ST_distance_spheroid. Obe vračata najkrajšo razdaljo v metrih. Prva računa neposredno na sferi s fiksnim polmerom 6.370.986 m, pri drugi pa sami izberemo elipsoid. Druga je natančnejša in zato počasnejša. Obe pa znata računati najkrajšo razdaljo samo med dvema točkama, ne pa tudi med linijami ali poligoni.
Osnovna poizvedba (varianta 1), ki najde najbližje naslove (naslovi so točke) od iskalne lokacije je naslednja:
from Address as a
where ST_distance_sphere(a.point, :point) <= :distance
order by ST_distance_sphere(a.point, :point)Koda 8.3: Poizvedba HQL, varianta 1: iskanje najbližjih naslovov, računanje razdalj v metrih na Zemlji (sferi). ":point" je iskalna lokacija, ":distance" je iskalni radij v metrih.
Poizvedba kliče funkcijo ST_distance_sphere, ki ne uporablja indeksov, zato je razmeroma počasna.
Zgornjo poizvedbo lahko s trikom precej pohitrimo. Ta najprej iskanje omeji na določeno območje - iskalni pravokotnik (angl. bounding box), nato pa računa razdalje samo še na tem delu (varianta 2):
from Address as a
where ST_Intersects(a.point, :bbox) = true
and ST_distance_sphere(a.point, :point) <= :distance
order by ST_distance_sphere(a.point, :point)Koda 8.4: Poizvedba HQL, varianta 2: iskanje najbližjih naslovov, računanje razdalj v metrih na Zemlji (sferi) z dodatnim iskalnim pravokotnikom. ":point" je iskalna lokacija, ":distance" je iskalni radij v metrih, ":bbox" je iskalni pravokotnik v stopinjah.
Pred tem je treba iskalni pravokotnik še izračunati. To storimo tako, da najprej iskalno lokacijo povečamo v smeri zemljepisne dolžine za iskalni radij in nato še v smeri zemljepisne širine. Iskalni radij je podan v metrih, zato si pri pretvorbi pomagamo s kotnimi funkcijami: iz razdalje v metrih izračunamo razdaljo v stopinjah. Ta je seveda različna za različne lokacije na Zemlji.
Takšen iskalni pravokotnik v funkciji PostGIS ST_Intersects ignorira vse točke (naslove), ki niso v njem oz. se ga ne dotikajo. Funkcija ST_Intersects uporablja indekse, saj se izvaja neposredno na točkah, ki so v stopinjah.
Ostali del poizvedbe je enak prvi varianti, le da se izvaja računanje razdalj med točkami na bistveno manjši množici. Zato je druga varianta bistveno hitrejša v primerjavi s prvo, medtem ko se natančnost ne poslabša. Hitrost se začne zmanjševati, če povečujemo iskalni radij, saj tedaj ST_Intersects ignorira vse manj točk.
Kot zanimivost sem preizkusil še tretjo varianto po metodi A, ki je tudi dovolj natančna, kadar je iskalni radij normalno majhen (tako kot v praksi):
from Address as a
where ST_DWithin(ST_Transform(a.point, :utm),
ST_Transform(:place, :utm), :distance) = true
order by ST_Distance(ST_Transform(a.point, :utm),
ST_Transform(:place, :utm))Koda 8.5: Poizvedba HQL, varianta 3: iskanje najbližjih naslovov, projekcija UTM. ":place" je iskalna lokacija, ":distance" je iskalni radij v metrih, ":utm" je številka SRID cone UTM.
Ta varianta obe točki, iskalno lokacijo in naslov, najprej projicira v coni UTM (funkcija PostGIS ST_Transform), v kateri je iskalna lokacija, in nato med njima izračuna razdaljo. Funkcija ST_DWithin ugotovi, ali sta točki preveč oddaljeni druga od druge.
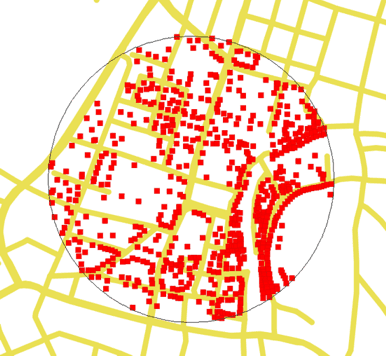
Pri tej poizvedbi se indeksi nikjer ne uporabljajo, saj je potrebno najprej vsako točko (naslov) projicirati, šele nato se lahko izvede primerjava. Ta varianta je zato počasna, še nekoliko bolj kot prva.
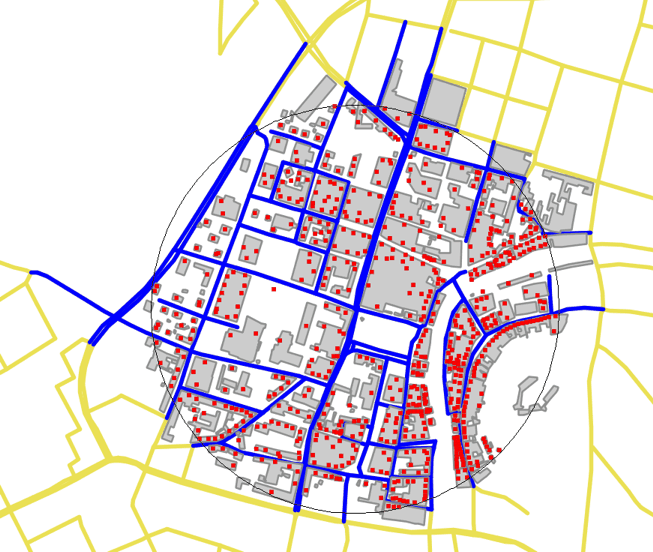
Slika 8.3: Rezultat poizvedb variante 1, 2 in 3 je enak in natančen. Rdeči kvadratki so najdeni naslovi, iskalni radij je 500 m (tanka črna krožnica), v središču Ljubljane.
Za primerjavo hitrosti sem preizkusil še četrto varianto po metodi Č, ki pa ji natančnost že kar pošteno peša, a je najhitrejša:
from Address as a
where ST_Intersects(a.point, :bbox) = true
order by ST_Distance(a.point, :place)Koda 8.6: Poizvedba HQL, varianta 4: iskanje najbližjih naslovov, primerjanje razdalj v stopinjah. ":place" je iskalna lokacija, ":bbox" je iskalni pravokotnik v stopinjah.
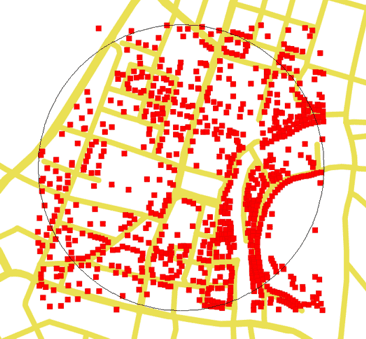
Ta, enako kot druga varianta, najprej izračuna iskalni pravokotnik (bbox) in pri obeh funkcijah ST_Intersects in ST_Distance uporablja indekse. Ker se primerjanje razdalj izvaja neposredno na točkah, ki so samo v stopinjah, je poizvedba bliskovito hitra, a nekoliko nenatančna, saj se razmerje med stopinjami in metri z zemljepisno širino spreminja. Poleg te napake vrne tudi vse točke, ki so v iskalnem pravokotniku in na vogalih niso omejeni z iskalnim radijem, kot je lepo vidno na sliki 8.4:
Slika 8.4: Rezultat poizvedbe variante 4 je nenatančen a najhitrejši. Rdeči kvadratki so najdeni naslovi, iskalni radij je 500 m (tanka črna krožnica), v središču Ljubljane. Nekateri najdeni naslovi presegajo iskalni radij.
Funkcija PostGIS ST_distance_sphere kot parametra vzame samo dve točki. Če želimo med seboj primerjati oddaljenost linije (npr. cesto) od točke, moramo najprej na liniji poiskati najbližjo točko iskalni točki. Z enako težavo se srečamo pri poligonu. Rešitev žal ni vgrajena v PostGIS, ampak jo z malce truda lahko sami razvijemo.
Poizvedba, ki poišče najbližjo cesto (linijo) iskalni točki, je naslednja:
from Street as s
where ST_Intersects(s.lineString, :bbox) = true
and ST_distance_sphere(:point,
ST_line_interpolate_point(s.lineString,
ST_line_locate_point(s.lineString, :point))) <= :distance
order by ST_distance_sphere(:point,
ST_line_interpolate_point(s.lineString,
ST_line_locate_point(s.lineString, :point)))Koda 8.7: Poizvedba HQL: iskanje najbližjih cest. ":point" je iskalna lokacija, ":distance" je iskalni radij v metrih, ":bbox" je iskalni pravokotnik v stopinjah.
Poizvedba je pravzaprav enaka tisti za naslove (varianta 2), le da je linija dodatno oplemenitena z dvema funkcijama PostGIS. Prva je ST_line_locate_point, ki vrne najbližjo točko (na liniji) med linijo in iskalno točko v obliki razdalje od začetne točke linije. Druga je ST_line_interpolate_point, ki pa točko na liniji dejansko izračuna iz podane razdalje. Tukaj je treba vedeti, da je točka na liniji interpolirana, ker je največkrat vmes, med definiranimi točkami, ki sicer opisujejo linijo (pravzaprav niz linij).
Ti dve funkciji se sicer zelo hitro izvajata, tako da na koncu celotna poizvedba ne odstopa veliko od tiste za iskanje naslovov.
Zadnja, ki jo storitev potrebuje, je poizvedba, ki poišče najbližjo zgradbo (poligon) iskalni točki:
from Building as b
where ST_Intersects(b.polygon, :bbox) = true
and ST_distance_sphere(:point,
ST_line_interpolate_point(ST_ExteriorRing(b.polygon),
ST_line_locate_point(ST_ExteriorRing(b.polygon), :point)))
<= :distance
order by ST_distance_sphere(:point,
ST_line_interpolate_point(ST_ExteriorRing(b.polygon),
ST_line_locate_point(ST_ExteriorRing(b.polygon), :point)))Koda 8.8: Poizvedba HQL: iskanje najbližjih zgradb. ":point" je iskalna lokacija, ":distance" je iskalni radij v metrih, ":bbox" je iskalni pravokotnik v stopinjah.
Poizvedba je na las podobna tisti za iskanje cest, a najprej iz poligona s funkcijo ST_ExteriorRing pridobi linijo. To je linija (pravzaprav niz linij), ki opisuje zunanji del poligona. Poizvedba deluje tako, da poišče najbližji poligon samo glede na zunanji obod poligona, kar ni nič slabega. Zgradbe so ponavadi majhne glede na iskalni radij, če pa iskalna točka pade točno v notranjost poligona, bo vseeno ta poligon najbližji.
Slika 8.5: Rezultat nasprotnega geokodiranja v središču Ljubljane. Rdeči kvadratki so naslovi, modre črte so ceste in sivi liki so zgradbe, ki jih je našel sestavljeni iskalec FullCompositeLocator z iskalnim radijem 500 m (tanka črna krožnica).
8.3 Zmogljivost
Najprej bom prikazal rezultate meritev hitrosti vseh štirih variant poizvedb za naslove. Parametre sem nastavil tako kot v praksi: iskalni radij na 5 km, zanimalo pa me je prvih deset naslovov. Vsako poizvedbo sem ponovil stokrat z enim zagonom okolja, vsako meritev pa trikrat. Poizvedbe so se vršile v lokalno nameščeni podatkovni zbirki.
| Varianta | Opis | Povprečni čas izvajanja poizvedbe | |
|---|---|---|---|
| 1 | razdalja v metrih na Zemlji | 610,00 ms | 64,3 % |
| 2 | razdalja v metrih na Zemlji omejena z iskalnim pravokotnikom | 22,45 ms | 2,4 % |
| 3 | projekcija UTM | 949,22 ms | 100,0 % |
| 4 | razdalja v stopinjah | 20,78 ms | 2,2 % |
Tabela 8.2: Rezultati meritve hitrosti vseh štirih variant za iskanje najbližjih naslovov. Manj je bolje.
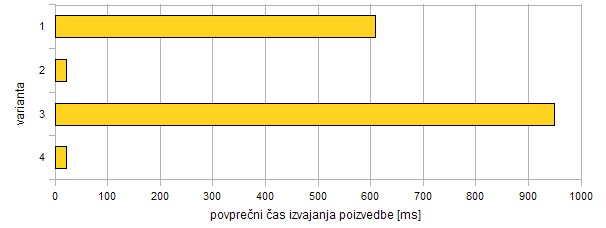
Graf 8.1: Rezultati meritve hitrosti vseh štirih variant za iskanje najbližjih naslovov. Manj je bolje.
Takoj opazimo občutne razlike v hitrosti izvajanja poizvedb, saj je varianta 1 kar 27-krat počasnejša od variante 2. Meritve so tokrat nazorno pokazale, kakšna je razlika v poizvedbi, ki se vrši z indeksi ali brez: pri variantah 2 in 4 se uporabljajo indeksi. Zanemarljiva, a opazna je razlika med varianto 2 in 4 (v povprečju ~ 2 ms): to lahko pripišemo funkciji ST_distance_sphere, ki se uporablja samo pri varianti 2 in ne uporablja indeksov nad sicer zelo zmanjšano množico točk.
Za časovni pribitek pri varianti 3 je vsekakor kriva funkcija ST_Transform, ki iskalno lokacijo in naslov najprej projicira.
Sledi meritev hitrosti izvajanja poizvedbe pri različnih iskalnih radijih (maxDistanceMeters), vedno pa vrne 10 zadetkov. Meritve sem opravil na variantah 1, 2 in 4.
| maxDistanceMeters | Varianta | Povprečni čas izvajanja poizvedbe |
|---|---|---|
| 1000 | 1 | 609,53 ms |
| 2 | 14,01 ms | |
| 4 | 12,97 ms | |
| 5000 | 1 | 610,00 ms |
| 2 | 22,45 ms | |
| 4 | 20,78 ms | |
| 10000 | 1 | 615,94 ms |
| 2 | 59,89 ms | |
| 4 | 50,63 ms | |
| 50000 | 1 | 980,89 ms |
| 2 | 1626,00 ms | |
| 4 | 1369,74 ms |
Tabela 8.3: Rezultati meritve hitrosti izvajanja poizvedbe za iskanje najbližjih naslovov pri različnih iskalnih radijih. Manj je bolje.
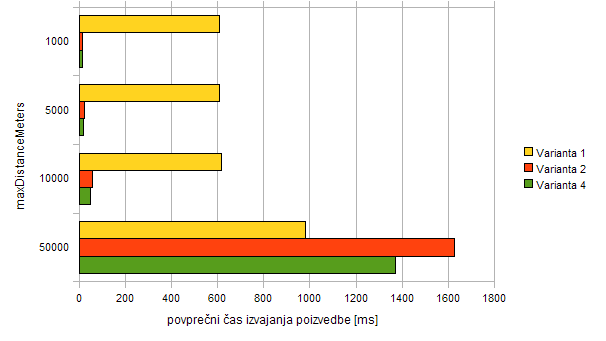
Graf 8.2: Rezultati meritve hitrosti izvajanja poizvedbe za iskanje najbližjih naslovov pri različnih iskalnih radijih. Manj je bolje.
Rezultati so rahlo presenetljivi.
Varianta 1 je najbolj predvidljiva, saj pri njej iskalni radij ne vpliva bistveno - vedno primerja vse naslove. Se pa vseeno malenkost hitrost zmanjša, kar lahko pripišemo sortiranju večje množice zadetkov. Sortiranje tako ali tako vpliva na hitrost pri vseh variantah.
Rezultati meritev pri varianti 2 so nepričakovani. Pričakoval sem zmanjšanje hitrosti z večanjem iskalnega radija vse tja do hitrosti variante 1, a je hitrost bistveno bolj padla. Odgovor ponuja kar meritev pri varianti 4, ki kaže, da funkcija ST_Intersects potrebuje svoj čas. Očitno večji iskalni pravokotnik resno upočasni funkcijo, vsaj na področju, kjer je veliko zadetkov. Varianti 2 in 4 sem pognal še z iskalno lokacijo, ki je bila na področju, kjer ni nobenega naslova daleč naokoli. Obe sta potrebovali tako rekoč nič časa ne glede na iskalni radij, kar je v redu.
Zanimivo pri vsem tem je, da je varianta 2 počasnejša od variante 1 pri velikem iskalnem radiju, kljub temu, da je bolj napredna. A zanimiva je meja. S poskušanjem sem ugotovil, da je meja pri iskalnem radiju nekje 35 km. Če je iskalni radij manjši, je varianta 2 hitrejša, če je večji, je varianta 1 hitrejša. Naj še poudarim, da to velja samo pri določenem število naslovov, ki so v iskalnem radiju (v mojem primeru jih je pri iskalnem radiju 35 km kar 99.624). Če iščemo najbližje naslove tam, kjer jih ni, potem bo varianta 1 še vedno potrebovala svoj čas, medtem ko se bo varianta 2 takoj izvedla.
Pri snovanju poizvedbe, ki jo uporablja storitev nasprotnega geokodiranja (varianta 2), bi lahko vgradili dodaten pogoj, da se funkcija ST_Intersects ne uporabi pri velikem iskalnem radiju, a je meja zelo različna in je ne moremo vedeti vnaprej. Poleg tega je meja na področju, kjer je veliko naslovov, razmeroma velika, tako da se v praksi ne uporablja.
V nadaljevanju bom prikazal, kako na hitrost poizvedbe vplivajo dodatne funkcije, ki so potrebne pri iskanju cest in zgradb. Meritve sem izvajal na enak način kot prej.
| Poizvedba | Povprečni čas izvajanja poizvedbe | |
|---|---|---|
| iskanje naslovov | 22,45 ms | 78,8 % |
| iskanje cest | 26,25 ms | 92,1 % |
| iskanje zgradb | 28,49 ms | 100,0 % |
Tabela 8.4: Rezultati meritve hitrosti izvajanja poizvedb. Manj je bolje.
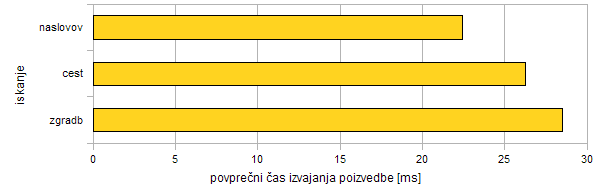
Graf 8.3: Rezultati meritve hitrosti izvajanja poizvedb. Manj je bolje.
Vse tri poizvedbe se izvajajo zelo hitro, za 4 ms in še za dodatne 2 ms počasnejši sta poizvedbi za iskanje cest in zgradb, za kar so krivi klici dodatnih funkcij, ki so potrebne pri iskanju najbližjega dela ceste oz. zgradbe iskalni lokaciji.
Pri testiranju zmogljivosti storitve sem, enako kot pri storitvi geokodiranja, izvedel trinivojsko meritev, ki je pokazala hitrostne razlike med tremi različnimi nivoji v sami arhitekturi storitve: DAO, storitev, odjemalec. Nivoji so nazorno prikazani na sliki 7.3.
Vse tri nivoje sem testiral na lokalnem računalniku. Parameter, ki sem ga spreminjal, je največje število zadetkov (maxResults). Vsak klic sem ponovil stokrat z enim zagonom okolja, vsako meritev pa trikrat.
Iskal sem naslove (varianta 2). Iskalni radij sem pustil na 5 km. Na nivojih storitve in odjemalca sem uporabil iskalca AddressLocator.
| maxResults | Nivo | Povprečni čas izvajanja klica |
|---|---|---|
| 1 | DAO | 21,67 ms |
| storitev | 21,93 ms | |
| odjemalec | 21,82 ms | |
| 10 | DAO | 22,45 ms |
| storitev | 31,41 ms | |
| odjemalec | 29,37 ms | |
| 100 | DAO | 26,46 ms |
| storitev | 107,81 ms | |
| odjemalec | 112,55 ms | |
| 1000 | DAO | 62,34 ms |
| storitev | 852,19 ms | |
| odjemalec | 893,60 ms |
Tabela 8.5: Rezultati trinivojske meritve zmogljivosti. Manj je bolje.
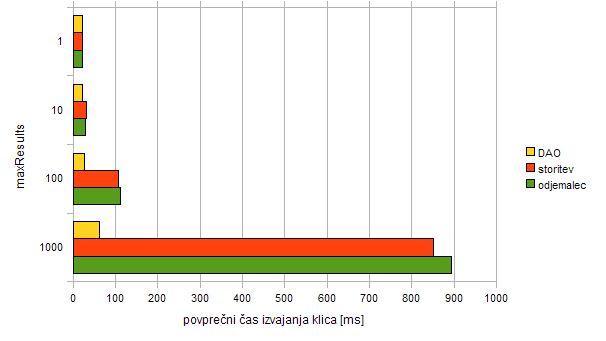
Graf 8.4: Rezultati trinivojske meritve zmogljivosti. Manj je bolje.
Rezultati slednje meritve kažejo na hitrost ostale infrastrukture, kajti sama poizvedba v podatkovni zbirki se je v vseh primerih izvedla enako hitro. Parameter maxResults namreč omeji le velikost rezultatov, ne vpliva pa nič na sortiranje v sami poizvedbi. Počasnejše izvajanje torej gre pripisati drugim dejavnikom, kot je prenašanje rezultatov med zbirko in programom. Še posebej se to pozna pri storitvi in odjemalcu, ki sta v primeru, da je največje število 1000, kar 14-krat počasnejša od DAO. To je posledica tega, da Hibernate vsak element posebej pograbi (angl. lazy fetch) iz zbirke šele po tem, ko se ga uporabi (nivo DAO ga ne uporabi). Pri trinivojski meritvi pri storitvi geokodiranja je že sama poizvedba (uporablja se združevanje tabel - join) pograbila (angl. eager fetch) vse podatke, zato so bili rezultati DAO bolj primerljivi s storitvijo in odjemalcem.
 §
§