Zahvala Kazalo Seznam uporabljenih kratic in simbolov 1 Povzetek 2 Abstract 3 Uvod 4 Opis problema 5 Načrt sistema 6 Podatkovni model 7 Geokodiranje 8 Nasprotno geokodiranje 9 Usmerjanje 10 Izkušnje in nadaljnje delo 11 Sklep Dodatek A Navodila za uporabo sistema Literatura
- Naslov
- Razvoj naprednih storitev za GIS
- Del
- 9 Usmerjanje
- Datum vsebine
- 22. 11. 2009
- Original
- RazvojNaprednihStoritevZaGIS.pdf
- Vrsta
- diplomska naloga
- Jezik
- slovenščina
- Različica
- 1.0
- Ustanova
- Fakulteta za računalništvo in informatiko, Univerza v Ljubljani
- Študij
- Univerzitetni, računalništvo in informatika, logika in sistemi
- Predmet
- -
- Mentor
- doc. dr. Mojca Ciglarič
- Avtor
- Tine Lesjak
- Ocena
- 10 od 1-10
Gre za celotno diplomsko delo s predstavitvijo.
Dodatne objave dela:
- ePrints.FRI: ID 933
- COBISS: ID 7349844
- predstavitev.pdf
- Predstavitev diplomskega dela na zagovoru (dne 22. 10. 2009).
- projekti.zip
- Vsa izvorna koda v obliki SpringSource Tool Suite projektov (združljivi z Eclipseom) pod licenco Creative Commons Attribution 2.5 Slovenia License
- primeri.zip
- Primeri, predstavljeni kot izvlečki kode v diplomskem delu.
- tinel-gis-geocoding.war
- Storitev geokodiranja.
- tinel-gis-reversegeocoding.war
- Storitev nasprotnega geokodiranja.
- tinel-gis-routing.war
- Storitev usmerjanja.
Algoritem za usmerjanje je bolj obširen in bolj zapleten, zato sem izkoristil edinstveno priložnost in se povezal s sošolcem in sodelavcem Ivanom Fućakom, ki je pred kratkim izdelal diplomsko delo na to temo [3]. Njegovo delo mi je pomagalo pri teoretičnem razumevanju, pri iskanju primernih rešitev in pri testiranju.
Usmerjanje je storitev, ki izračuna najcenejšo pot iz lokacije A v lokacijo B. Uporabniki lahko to pot primerjajo s svojo trenutno ali pa načrtujejo povsem novo. Pri tem lahko izbirajo, kaj jim pomeni najcenejša pot.
Ustrezna koda se nahaja v javinem paketu net.tinelstudio.gis.routing.
9.1 Algoritem
Usmerjanje implementira usmerjevalni algoritem A* (angl. izgovorjava "A star"), ki ga ovija v uporabno storitev. Algoritem A* je najbolj priljubljena izbira pri iskanju poti. Spada med algoritme za iskanje najkrajših poti pri grafih (angl. graph search algorithm).
Za usmerjanje je bilo treba rahlo prilagoditi podatkovni model, ki vsebuje nekaj novosti, ki jih uporablja samo usmerjevalni algoritem.
Nov je domenski objekt StreetNode, vsebuje pa vsa vozlišča vseh cest, to so začetne in končne točke vsakega odseka ceste.
Domenski objekt Street je dobil naslednje nove atribute:
- lengthMeters - dolžina odseka ceste v metrih,
- level - nivo ceste,
- oneWay - enosmernost ceste,
- startNode - začetno vozlišče in
- endNode - končno vozlišče.
Sam usmerjevalni algoritem A* sem implementiral povsem na novo. Preprost opis algoritma se nahaja na spletni enciklopediji Wikipedia v obliki psevdokode [6] in na spletni strani gospoda Amita [5]. Amitov algoritem je za odtenek boljši, saj nudi večji delovni razpon.
Algoritem A* je pravzaprav preprost. Sprehodi se po cestah od začetnega do ciljnega vozlišča. Pri tem za izračun optimalne poti uporablja dve vrsti ocenjevanja.
Na eni strani računa ceno že obdelane poti g(n), na drugi strani pa hevristično išče najcenejšo smer proti ciljnemu vozlišču h(n). Če seštejemo oboje skupaj, dobimo ceno celotne poti, ki gre skozi neko vmesno vozlišče n:
f(n) = g(n) + h(n) (9.1)V kolikor je cena te poti, recimo ji A, višja od cene poti, recimo ji B, ki gre, npr., skozi drugo vmesno vozlišče m, se za nadaljnjo obravnavo vzame pot B. To traja tako dolgo, dokler algoritem ne pride do ciljnega vozlišča.
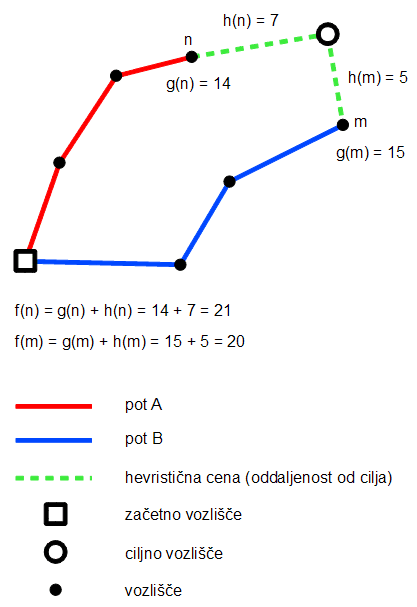
Slika 9.1: Algoritem A* išče najcenejšo pot. Pot A, ki gre skozi vozlišče n, je dražja (f(n) = 21) od poti B, ki gre skozi vozlišče m (f(m) = 20), zato se za nadaljnjo obravnavo vzame cenejša pot B.
Od zunaj tako lahko nastavljamo obe pomembni funkciji: ceno že obdelane poti g(n) in hevristično ceno neznane poti do ciljnega vozlišča h(n). S tema dvema funkcijama lahko fino nastavljamo obnašanje algoritma. Pot lahko izračuna izredno hitro in razmeroma slabo (ne absolutno najcenejšo), ali pa zelo počasi in zajamčeno najcenejšo (kot algoritem Dijkstra).
Kaj šteje za ceno poti je lahko določeno različno: lahko šteje le razdalja, ali pa se tudi upošteva nivo ceste (npr. avtocesta je cenejša, ker je v praksi hitrejša in enostavnejša).
Poglejmo, kako te dve funkciji vplivata na obnašanje algoritma A*:
- V eni skrajnosti lahko nastavimo, da hevristična funkcija h(n) vedno vrne 0. Algoritem se spremeni v Dijkstra in zajamčeno najde najcenejšo pot. Pri tem je najbolj počasen.
- Če je h(n) vedno manjša ali enaka od prave cene od vozlišča n do ciljnega vozlišča, potem algoritem še vedno zajamčeno vrne najcenejšo pot. Manjši kot je h(n), počasnejši je.
- Če je h(n) vedno enaka od prave cene od vozlišča n do ciljnega vozlišča, potem se algoritem obnaša perfektno in je zelo hiter. Vendar je pravo ceno zelo težko vedeti vnaprej (zato raje hevristična ocena). To bi bilo možno samo, če bi, npr., vnaprej izračunali ceno med vsakima dvema vozliščema.
- Če je h(n) kdaj večji od prave cene od vozlišča n do ciljnega vozlišča, potem algoritem ne bo vedno našel najcenejše poti, ampak bo zelo hiter.
- V drugi skrajnosti, če je h(n) vedno precej večji od g(n), potem cel algoritem sloni samo na h(n) in se obnaša kot metoda požrešno najprej najboljši (angl. greedy best-first search).
9.2 Storitev
Storitev usmerjanja je zasnovana tako, da odjemalec strežniku poda zahtevo s štirimi parametri:
- začetno lokacijo,
- ciljno lokacijo,
- funkcija ocenjevanja že obdelane poti g(n) in
- funkcijo hevrističnega ocenjevanja še neobdelane poti h(n).
Začetna lokacija in ciljna lokacija sta točki, podani v geografskih koordinatah z zemljepisno dolžino in širino v stopinjah.
Storitev pozna dve uporabni implementaciji funkcije g(n):
- LengthCostFunction - Vrne ceno, ki je enaka pravi dolžini poti v metrih (iz atributa lengthMeters domene Street).
- LevelLengthCostFunction - Vrne ceno, ki je enaka dolžini poti v metrih pomnoženi z utežjo glede na nivo ceste (iz atributa level domene Street). Uporabnik mora vnaprej pripraviti uteži za vse nivoje cest.
Za funkcijo h(n) se običajno uporabljajo različne hevristike: razdalja Manhattan, diagonalna razdalja, evklidska razdalja, kvadratna evklidska razdalja in bolj zahtevne. Vsem je skupno to, da so namenjene iskanju poti po mreži. V našem primeru je mreža zemeljska obla (poenostavljeno sfera), ki ima neskončno majhne kvadratke (stopinje zemljepisne dolžine in širine). Ker zemljepisna dolžina in širina nista sorazmerni in je mreža neskončno majhna, je uporaba preprostih funkcij za računanje razdalj nesmiselna. Zato sistem pozna le eno primerno fleksibilno funkcijo h(n):
- GreatCircleDistanceHeuristicFunction - Vrne ceno poti glede na razdaljo med dvema vozliščema na sferi (Zemlji). Hkrati omogoča nastavljanje uteži, ki se pomnoži s to razdaljo. V primeru, da je utež enaka 1, je cena enaka razdalji.
Ker sta začetni in ciljni lokaciji podani v geografskih koordinatah, mora storitev najprej poiskati njima najbližja vozlišča. Način iskanja je isti kot pri iskanju najbližjih naslovov pri storitvi nasprotnega geokodiranja, le da se tokrat namesto naslovov iščejo vozlišča (domena StreetNode).
from StreetNode as sn
where ST_Intersects(sn.point, :bbox) = true
and ST_distance_sphere(sn.point, :point) <= :distance
order by ST_distance_sphere(sn.point, :point)Koda 9.1: Poizvedba HQL: iskanje najbližjih vozlišč. ":point" je iskalna lokacija, ":distance" je iskalni radij v metrih, ":bbox" je iskalni pravokotnik v stopinjah.
Storitev kot rezultat vrne celotno pot v obliki seznama odsekov cest (z vsemi atributi). Poleg tega vrne še ceno celotne poti in porabljen čas algoritma v milisekundah.
Coordinate startLocation=new Coordinate(14.596, 46.112);
Coordinate goalLocation=new Coordinate(15.100, 46.369);
Cost cost=new LengthCost();
Heuristic heuristic=new GreatCircleDistanceHeuristic(1.2);
Route route=this.routingService.findRoute(startLocation, goalLocation,
cost, heuristic);Koda 9.2: Primer uporabe storitve usmerjanja.
9.3 Zmogljivost
Pri storitvi usmerjanja sam algoritem ne teče kot ena poizvedba v podatkovni zbirki, pač pa potrebuje cestne odseke. Ko obdela en odsek ceste, iz zbirke zahteva vse odseke, ki se navezujejo na ta odsek (po vozliščih). Poizvedba upošteva tudi enosmernost cest.
from Street
where startNode = ? or (oneWay = false and endNode = ?)Koda 9.3: Poizvedba HQL, ki najde vse cestne odseke, ki se začnejo (prvi "?") ali končajo (drugi "?") v podanem vozlišču. Pri tem upošteva morebitno enosmernost odseka.
Meritve, ki sem jih opravil, kažejo ravno na to poizvedbo, saj porabi praktično ves čas algoritma.
Pri meritvah sem spreminjal hevristično funkcijo oz. njeno utež, saj je v vseh primerih nastopala GreatCircleDistanceHeuristic:
- Pri uteži 0 (vsa vozlišča so enako oddaljena od cilja), algoritem deluje kot Dijkstra in vedno najde najcenejšo pot na račun počasnosti.
- Pri uteži 1 (vsa vozlišča so od cilja oddaljena toliko, kot znaša zračna razdalja), algoritem še vedno v večini primerov najde najcenejšo pot, vendar svoje delo opravi občutno hitreje.
- Pri uteži 1,2 (vsa vozlišča so od cilja oddaljena 20 % več, kot znaša zračna razdalja), algoritem najde poceni pot in je pri tem razmeroma hiter. Ta utež se mi zdi najbolj primerna.
- Pri uteži 3 (vsa vozlišča so trikrat dlje od cilja, kot znaša zračna razdalja), algoritem išče pot vedno v najbolj ravni črti od začetka do cilja. Pri tem je zelo hiter, a redko vrne uporabne rezultate.
Spreminjal sem tudi funkcijo g(n) in sicer sem enkrat za ceno uporabil le pravo dolžino ceste ("dolžina"), funkcijo LengthCost, drugič pa je bila cena odvisna tudi od nivoja ceste ("hitrost"), funkcija LevelLengthCost. Ceno posameznega nivoja ceste, v podatkovni zbirki sem imel tri, sem nastavil tako, da so bile važnejše ceste najcenejše (ker so običajno najhitrejše), najmanjše pa najdražje (ker so običajno najpočasnejše).
Pri merjenju sem algoritem pognal tridesetkrat z enim zagonom okolja, vsako meritev pa trikrat. Začetna lokacija je bila v Škofljici, ciljna pa v Ljubljana-Dravlje.
| h(n) utež | g(n) | Povprečni čas izvajanja algoritma | Število poizvedb |
|---|---|---|---|
| 0 | dolžina | 4227,09 ms | 3343 |
| hitrost | 4640,28 ms | 3576 | |
| 1 | dolžina | 930,21 ms | 578 |
| hitrost | 1235,40 ms | 837 | |
| 1,2 | dolžina | 375,00 ms | 158 |
| hitrost | 990,45 ms | 645 | |
| 3 | dolžina | 258,33 ms | 70 |
| hitrost | 246,88 ms | 69 |
Tabela 9.1: Rezultati meritve hitrosti algoritma A* in števila poizvedb pri različnih utežeh hevristične funkcije h(n) in dveh različnih funkcijah ocenjevanja že obdelane poti g(n).
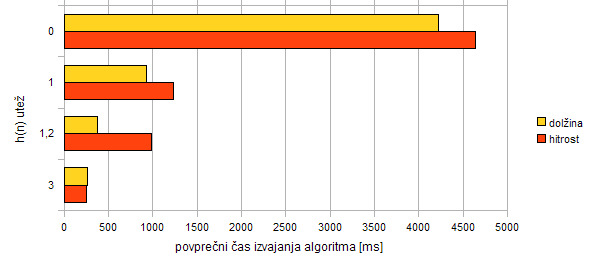
Graf 9.1: Rezultati meritve hitrosti algoritma A* pri različnih utežeh hevristične funkcije h(n) in dveh različnih funkcijah ocenjevanja že obdelane poti g(n).
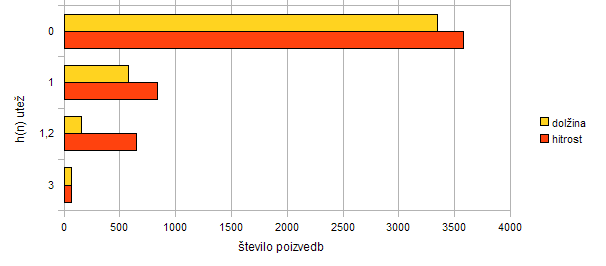
Graf 9.2: Rezultati meritve števila poizvedb algoritma A* pri različnih utežeh hevristične funkcije h(n) in dveh različnih funkcijah ocenjevanja že obdelane poti g(n).
Oblika grafa 9.1, ki ponazarja hitrost algoritma, je zelo podobna obliki grafa 9.2, ki ponazarja število poizvedb. To pomeni, da je hitrost algoritma odvisna samo od števila poizvedb. Možna izboljšava algoritma bi bila, da bi iz baze potegnil odseke cest večjega območja okoli podanega vozlišča, nekakšen iskalni pravokotnik. S tem bi sicer upočasnili samo poizvedbo, a bi se število le-teh občutno zmanjšalo. Namesto sedanjih 3343 pri prvem testu, bi za to pot bile dovolj le, recimo, štiri.
Zanimivo je, da algoritem v našem primeru izračuna povsem enake poti pri hevrističnih utežeh 0 in 1. A je pri uteži 1 do 4,5-krat hitrejši! Pri uteži 1,2 je algoritem še hitrejši, pri tem pa so razlike v poti minimalne, a pot ni več absolutno najcenejša.
Zanimiva je tudi velika razlika pri hevristični uteži 1,2 med potjo "dolžina" in med potjo "hitrost". Slednja se namreč skoraj trikrat počasneje izračuna. Razlog tiči v rezultatu, ki je lepo viden na sliki 9.2. Pot "hitrost" nas iz Škofljice v Ljubljana-Dravlje pripelje po avtocesti, medtem ko pot "dolžina" vodi skozi center Ljubljane. Pri tem je izračun poti "hitrost" na meji med tem, ali bi tekla po avtocesti, ali skozi center. Namreč, če nastavimo hevristično utež na 1,5, že prevlada pot skozi center.
Slika 9.2: Rezultat usmerjanja iz Škofljice v Ljubljana-Dravlje. Pot "hitrost" (zelena črta) nas pripelje po avtocesti, medtem ko pot "dolžina" (modra črta) vodi skozi center Ljubljane. Na začetku in na koncu se poti prekrivata. Utež h(n) je bila v obeh primerih 1,2. Na sliki so lepo vidni nivoji cest. Ceste najvišjega nivoja so oranžne, srednjega rumene in najnižjega sive. V primeru poti "hitrost" to pomeni, da so oranžne črte najcenejše (najhitrejše), sive pa najdražje (najpočasnejše).
Pri testiranju zmogljivosti storitve sem izvedel trinivojsko meritev, ki je pokazala hitrostne razlike med tremi različnimi nivoji v sami arhitekturi storitve:
- Algoritem - Neposreden klic algoritma, ki izračuna pot.
- Storitev - Klic storitve, ki pripravi posredovane iskalne podatke (poišče začetno in ciljno vozlišče) in pokliče algoritem.
- Odjemalec - Klic storitve prek HTTP Invokerja na zagnan strežnik storitve.
Vse tri nivoje sem testiral na lokalnem računalniku (testi, strežnik in zbirka so tekli lokalno). Vsak klic sem ponovil tridesetkrat z enim zagonom okolja, vsako meritev pa trikrat.
Začetna lokacija je bila v Škofljici, ciljna pa v Ljubljana-Dravlje. Funkcija h(n) je bila GreatCircleDistanceHeuristic z utežjo 1,2. Funkcija g(n) je bila LevelLengthCost s primerno utežnimi nivoji: važnejše ceste so najcenejše, manjše so najdražje.
| Nivo | Povprečni čas izvajanja klica | |
|---|---|---|
| algoritem | 990,45 ms | 92,19 % |
| storitev | 1074,30 ms | 100,00 % |
| odjemalec | 1008,84 ms | 93,91 % |
Tabela 9.2: Rezultati trinivojske meritve zmogljivosti. Manj je bolje.
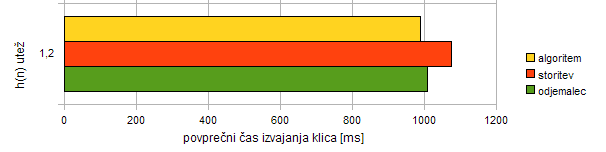
Graf 9.3: Rezultati trinivojske meritve zmogljivosti. Manj je bolje.
Rezultati meritve kažejo na hitrost celotne infrastrukture. Storitev in odjemalec sta pričakovano nekoliko počasnejša od golega algoritma, kar je posledica dodatnih funkcij, ki jih opravita (predvsem iskanje začetnega in ciljnega vozlišča). Zanimiv pa je odjemalec, saj je hitrejši od storitve. To je posledica tega, da je strežnik skozi vse meritve tekel in si je tako že napolnil predpomnilnik (angl. cache). Komunikacija med strežnikom in odjemalcem (protokol HTTP) pa očitno ne vpliva toliko, kar je posledica tega, da sta strežnik in odjemalec tekla lokalno, na istem računalniku.
 §
§